Pythagoras Theorem

If the diagonals of a rhombus are $8 \mathrm{units}$ and $6 \mathrm{units}$, then the square of its side is ;

A ladder $20 \mathrm{m}$ long is placed in street so as to reach a window $16 \mathrm{m}$ high. On turning the ladder on the other side of the street, it reaches a point $12 \mathrm{m}$ high.The width of the street is ; 

The length of the hypotenuse of a right-angled triangle, having equal base and height and the area of the triangle is $128 {\mathrm{cm}}^2$ is :

$\mathrm{A}, \mathrm{B}$ and $\mathrm{P}$ are the three non-collinear points on a plane. The distance between the point $\mathrm{A}$ and $\mathrm{P}$ is $2 \mathrm{m}$ more than the distance between the points $\mathrm{B}$ and $\mathrm{P}$. If the distance between points $\mathrm{A}$ and $\mathrm{B}$ is $10 \mathrm{m}$ and $\mathrm{AB}$ is the longest side of the triangle $\mathrm{ABC}$. Is $\mathrm{ABC}$ is a right-angled triangle or not, Justify your answer using the discriminant of quadratic equation and also find the measure of $\mathrm{AP}$ and $\mathrm{BP}$.

One end of a string $24 \mathrm{m}$ long is attached to the top end of a vertical pillar $18 \mathrm{m}$ high. The other end of that wire is attached to the nail. At what distance from the base of the pillar the string is taut.

A congruent side of an isosceles right-angled triangle is $7 \mathrm{cm}$ ,Find its perimeter.

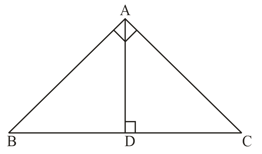
In the figure, $ABC$ is a right-angled triangle and $\angle BAC=90°$. If $AD\perp BC$ and $BD=DC$, then prove that ${\mathrm{BC}}^2=4{\mathrm{AD}}^2$.

The picture below shows a staircase outside a house. Each step of the staircase is congruent and there are $25$ steps in the staircase from the floor to the platform and $25$ steps from the platform to the roof.

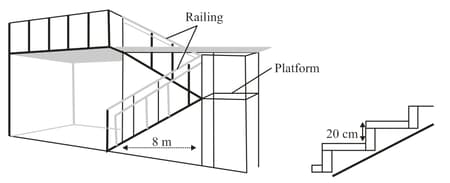
What is the length of the staircase railing?

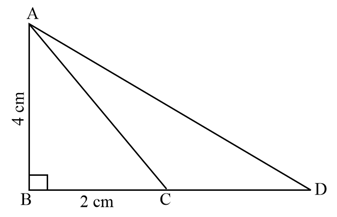
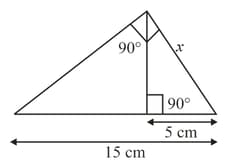
Find the value of $QT$ in the following figure:

Equilateral triangle $ABC$ is inscribed in a circle. If side of the triangle $= 24cm$, then the radius is

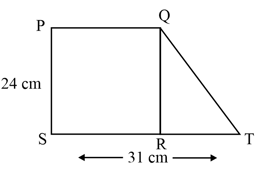
In the figure below, $XYZ$ is a right-angled triangle. $A$, $B$ and $C$ are the three points on $YZ$ such that they divide $YZ$ into $4$ equal parts.

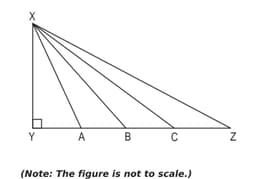
Prove that $3X{A}^2+X{B}^2+X{C}^2-X{Z}^2=4X{Y}^2$

Is it possible to have an isosceles right-angled triangle, such that the length of each of its sides is an integer? Give a reason to support your answer.

In $∆\mathrm{ABD}, \mathrm{AB}\perp \mathrm{BD}$ and $\mathrm{AC}=\mathrm{BD}$. If $\mathrm{AB}=4 \mathrm{cm}, \mathrm{BC}=2 \mathrm{cm}$, find $\mathrm{AD}$ (in $\mathrm{cm}$).

During a mathematics class, a teacher wrote the following three algebraic expressions on the board:
$\left(m^2-n^2\right),\left(2mn\right)\text{ and }\left(m^2+n^2\right.$, where $m$ and $n$are positive integers with $n<m$
One of the students, Kaivalya, claimed that the above set of expressions ALWAYS represent the sides of a right-angled triangle.
Is Kaivalya's claim correct? Justify your answer.

Abhilasha wants to find the radius of a circle. She places a set-square on the circle as shown below.

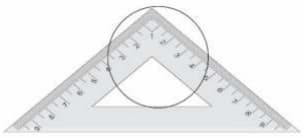
Based on the position of the set-square and the readings shown on the set-square, what is the diameter of the circle?

Two overlapping right triangles are shown below. What is the value of ‘$\mathrm{x}$’?

The sine of an angle in a right triangle is $\frac{4}{5}$.

Which of these could be the measures of the sides of the triangle? 

If the area of a square $ABCD\text{ is} 36 {\mathrm{cm}}^2$, then the area of the square obtained by joining the midpoints of the sides of the square $ABCD$ is:

Starting from the same point in a levelled field, Rahul walked $1000 \mathrm{m}$ towards East and then $1000 \mathrm{m}$ towards North whereas Aryan walked $2000 \mathrm{m}$ towards North-East. What is the distance between them now? (Take $\sqrt{2}=1.414$)

$PQR$ is an isosceles triangle inscribed in a circle. If $PQ= PR= 25 \mathrm{cm}$ and $QR= 14 \mathrm{cm}$, calculate the radius of the circle to the nearest $\mathrm{cm}$.